Exposing the Gambler's Fallacy
October 2021
You're playing roulette, and red has just come up eight times in a row! Now's the time to bet on black, right? Wrong. Red and black are equally likely. Even though we've just seen a bunch of reds. How can this be? Let's find out.
The gambler's fallacy is the mistaken belief that some result becomes more likely (or less likely) because of what happened before. The reality is that for most casino games, the odds don't actually change. Here are some examples.
- MYTH: In craps, if seven hasn't come up
for a while, it's about to come up because it's "due".
REALITY: Nothing is ever "due" in a random game. Seven is equally likely on every roll, regardless of how long the dry spell has been.
- MYTH: Once someone hits a slot machine
jackpot, that machine becomes less likely to hit a jackpot for a
while.
REALITY: Every spin has an equal chance of hitting the jackpot, regardless of whether the last jackpot was hit on the very last spin, or thousands of spins ago.
- MYTH: You're trying to come up with a betting
system, and you think the chances of success are better if
you choose when to bet (or when not to bet) based on streaks.
REALITY: What happened before has no bearing on what's going to happen next. If it did, then casino games would be easy to beat. Sitting out at inopportune times or jumping in at opportune times doesn't help, because you can't know when the inopportune or opportune times are. - MYTH: If you flip a coin and get 55 heads
and 45 tails, then if you keep flipping, the number of heads and
tails will eventually balance out.
REALITY: There's no force compelling the numbers to balance. For the next billion flips, the expectation is 500 million heads and 500 million tails (not 499,945 heads and 500,055 tails). The numbers *could* balance out, but nothing suggests that they should. - MYTH: The next ten spins in roulette are
more likely to be R R b R b b b R b R than ten reds.
REALITY: Each is equally likely. I know, this one is hard to wrap your head around. We'll get to that one in the discussion below.
Let's see why the fallacy seems to be right, and why it's actually not. We'll use coin flips because they're easy to understand.
We'll start with two things you already know: the chances of getting heads on a single coin flip is 1/2, and it's unlikely you'll get a bunch of heads in a row. For example, here are the chances of getting ten heads in a row:
![]() x
x ![]() x
x ![]() x
x ![]() x
x ![]() x
x ![]() x
x ![]() x
x ![]() x
x ![]() x
x ![]() =
= ![]()
That's 1 in 1,024. Not very likely, of course.
So here's where the gambler's fallacy comes in: Say you've tossed the coin nine times and amazingly, you got nine heads. You figure that the next toss will be tails, because the probability of getting ten heads in a row is one in 1024, which is really unlikely to happen.
The problem with this reasoning is that you're not looking at the chances of getting ten heads in a row, you're looking at the chances of getting one heads in a row. The heads that already happened no longer have a 50% chance of happening, they already happened. When you flip again the odds for that flip will be 50-50, same as it ever was.
Let's introduce our hero, Mr. P ("P" for "probability"). He'll always be looking to the future to see what's going to happen. Here he's about to make ten coin flips, hoping to get ten heads. Here's his outlook:

Mr. P, lucky guy that he is, got nine heads in a row. Here he is, getting ready to make his tenth flip:
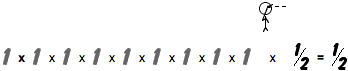
Now you're saying, Hey, wait! How come all the 1/2's turned into 1's? The answer is that they're no longer unknowns. Before you flip a coin you don't know what's going to happen so you have 50-50 odds. But after you flip the coin you definitely know what happened! After you flip a coin, the probability that you got a result is 1. You definitely flipped the coin. Definitely, definitely, as Rain Man would say. So after you've flipped nine heads, the probability of flipping a tenth head is 1x1x1x1x1x1x1x1x1x 1/2 = 1/2.
Let's have another look at Mr. P:
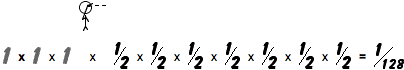
Notice that it doesn't matter where on the line you stick him, the chances of his next flip being heads is always 1/2. Wherever he is, it doesn't matter what happened before, his chances on his next toss are always 1 in 2.
How could it be otherwise? When you flip a coin you will get one result out of two possible outcomes. That's 1 in 2, or 1/2. Why and how could those numbers change just because you got a bunch of heads or tails already? They couldn't. The coin has no memory, it neither knows nor cares what was flipped before. If it's a 1-out-of-2 coin, it will always be a 1-out-of-2 coin.
Still not convinced? Then here's another way to think about it: Let's say someone hands you a coin and asks, "What are the chances of flipping heads?" Without hesitation you'd probably say 1 out of 2. But wait a minute—if it were true that heads were more likely if tails has just come up a bunch of times, then why did you answer "1 in 2" right away when asked about the chances of getting heads? Why didn't you say, "Well, first you have to tell me whether tails has been coming up a lot before I can tell you whether heads has a fair shot or not."? It's simple: You didn't ask about the previous flips because intuitively you know they're unimportant. If someone hands you a coin, the chances of getting heads are 1 in 2, regardless of what happened before.
Would it really be the case that you answered "1 in 2," and then your friend said, "Oh, I forgot to tell you, tails has just come up nine times in a row." Would you now suddenly change your answer and say that heads is more likely? I hope not.
One last example: Let's say your friend slides two quarters towards you across the table. She tells you that the first coin has been flipping normally, but the second quarter has just had nine tails in a row. Would you now believe that the chances of getting heads on the first coin are even but the chances of getting heads on the second coin are greater? Given two identical coins, could you really believe that one would be more likely to flip heads than the other? I hope not!
The same concept applies to roulette. An American roulette wheel has 18 red spots, 18 black spots, and 2 green spots. The chances of getting red on any one spin are 18/38. If you just saw nine reds in a row, what is the likelihood of getting black on the next spin?
18/38, same as it ever was.
The casino is playing you
Casinos are only too happy for you to buy into the gambler's fallacy. That's why they put an LED marquee on the roulette table showing what numbers have hit recently, and why they give baccarat players pads and pencils to track the results. They're not afraid to do that because they know that tracking what happened before is completely useless. Come on, are the casinos really gonna help you win?! Of course not. The fact that they're willing to help you track results should be an obvious red flag. They're hoping you fall for the fallacy and play longer, trying to chase a non-existent streak. Forewarned is forearmed. Don't fall for it!
Why R R b R b b b R b R in roulette is just as likely as ten reds
Here's a typical example of someone getting sucked into the gambler's fallacy because it seems reasonable. This was a post on an online gambling forum:
"Another example to show how useless
those mainstream gambling math theories are is that first they claim
that all even money bets have equal odds, and then the very same
math 'gurus' claim that this sequence: R R R R R R R R R R has
equal probability with this: R R b R b b b R b R. The first
statement contradicts the second and it's very obvious. Thus
there is a serious flaw in your perception. I suggest you to
reconsider from scratch all those mainstream and generic probability
theories because they have no value in action but only on papers." (source)
That's simply wrong. The math does describe how it happens in action, not just on paper. And these aren't "theories", as in unproven ideas, they're ironclad fact.
The mixed pattern of reds and blacks seems more likely, because normally when you play that's what you see: a mixed pattern of reds and blacks. You almost never see ten reds in a row. So, because you normally see mixed reds and blacks, our critic figured that getting that pattern of mixed reds and blacks is way more likely than ten reds.
The problem is that our critic chose a specific pattern of reds and blacks. Any specific pattern of ten mixed reds/blacks is just as likely as ten reds. Let's assume a wheel with no green spots, just reds and blacks, to make the discussion easier. Going through the critic's specific pattern, what's the chance of getting the first red? It's 1/2, of course. How about the second red? Also 1/2. For the third result, black, what are the chances? Again, 1/2. And so on. It doesn't matter whether our result is supposed to be red or black, the chances of either one are 50-50. You multiply out those ten 50-50 chances, your results are 1 in 1024, no matter whether the pattern is RRbRbbbRbR, RRRRRRRRRR, bbbbbRRRRR, or anything else.
To prove this, I programmed a simulator, below.
It spins a bunch of times and tells you how often each pattern came
up. Go ahead, try it.
| Chances of Unique Patterns in Roulette (excluding green 0/00) |
|
| Pattern | |
| Number of Sessions | |
| |
|
What it shows is that the mixed pattern is no more likely than the same number of reds in a row. (If your test showed otherwise, that's because there's some variance after only 100,000 spins. Run it again.)
The first set of results is for a bunch of sessions with exactly as many spins as is in the pattern. If you've been following along, you probably won't be surprised that the chances for our pattern are the same as for a bunch of reds in a row.
The second set of results treats all the spins as a single huge session. Here again, the mixed pattern and the all-reds pattern have the same chances.
The third set is why our critic got snookered by the fallacy. It shows that a set of ten mixed reds/blacks is way more likely than ten reds. Our critic thus thought that this meant that his specific pattern of reds/blacks was more likely than ten reds, but that's not the case. Once you have a specific pattern, the chances are the same as for ten reds. The simulator proves it.
I didn't always get this
If you used to believe in the gambler's fallacy, don't feel bad, because you're not alone. Lots of people get snagged by the fallacy. I used to be one of them. I can remember four distinct incidents in which I bought into it.
- In 7th grade, my math teacher Mr. Hall was reading math puzzles to the class. One of them was probably something like, "After flipping heads three times in a row, what are the chances of getting tails on the next flip?" After a pause, he announced, "Fifty percent, of course." I was thinking, "Wait, what? Why?" But he'd already moved on to the next problem. I remember thinking it seemed like a paradox: coin flips should always be 50-50, but doesn't three heads in a row mean something? (It doesn't.)
- In 12th grade, I was wondering if tails would be likely after two heads. My school had just gotten computers (1984) and I'd learned some programming, so I wrote a program to flip coins. The result: after two heads, the next flip was equally likely to be heads or tails. While this convinced me, I still didn't understand that similar misconceptions are part of the gambler's fallacy.
- At age 19 in college, I opined to my then-girlfriend that it should be safer to fly after a major crash, since two major crashes in a short period of time were unlikely. She immediately got very animated, insisting, "That's not the way it works!", and trying to explain it to me. She was very confident and certainly seemed to know what she was talking about, so I believed her, but I still didn't get a big-picture understanding of the fallacy.
- At age 33 I became interested in casino gambling. It seemed reasonable to sit in a casino and watch others play slots to figure out about how many hours it took to hit a jackpot, then wait until someone had played a machine close to that amount of time without hitting, then start playing myself when the slot was close to hitting. Of course, this doesn't work because a slot never gets closer to hitting, as every spin is random.
Well, that's all embarrassing, but at least now I know better. And so now I'm spreading the word.

